自1960年代以来，合成水凝胶已被开发并广泛应用于组织工程、药物运输、医用粘接剂、生物电子、亲水涂层、柔性机器人等。在许多承载的应用场景中，要求水凝胶能够承受长期的循环载荷，例如，人工心脏瓣膜每年需要打开和关闭约3亿次；膝盖关节软骨需承受幅值约2.5MPa的循环应力；透明扬声器之类的水凝胶离子设备需要承受高频振动；可拉伸的离子触摸板需要承受周期性变形。在循环载荷作用下，水凝胶会表现出疲劳特征，包括模量、强度的退化，内部裂纹的成核和生长等。近年来，哈佛大学锁志刚教授与西安交通大学软机器实验室团队在水凝胶疲劳领域开展了深入的研究，在水凝胶疲劳性能的实验测试与理论分析^[1]、疲劳门槛值的提升策略^{[2, 3]}、界面抗疲劳设计^{[4, 5]}等方面取得研究进展。

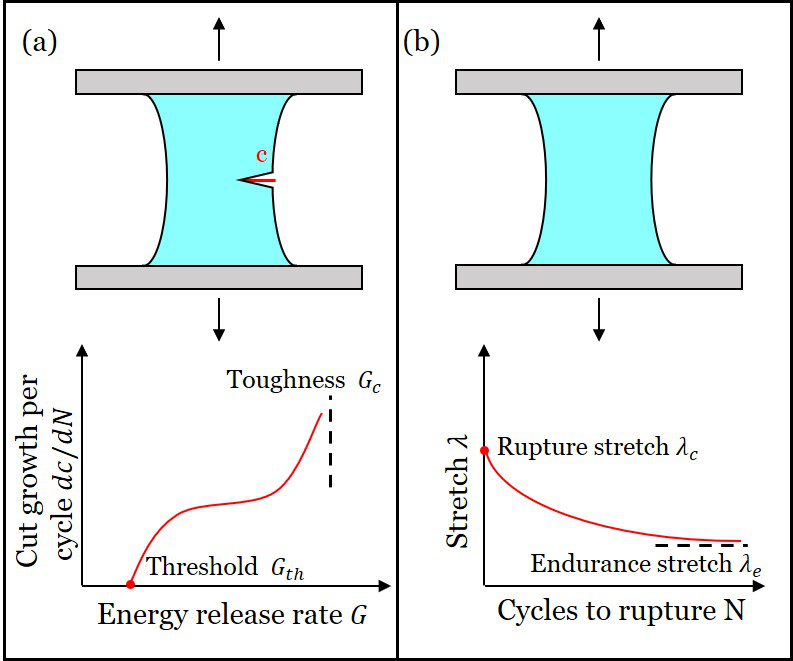
图1 两种疲劳测试方法。(a)预置裂纹的试样受到循环拉伸，记录在不同能量释放率下裂纹扩展的速率。(b)无预置裂纹的试样受到循环拉伸，记录在不同拉伸幅值λ下试样循环直至断裂的循环次数N。

  材料的疲劳测试主要有两大类方法。一种是在试样中预置裂纹，施加循环载荷并记录裂纹扩展速率（图1a）。当施加的能量释放率G低于疲劳门槛值G_th时，裂纹不扩展。从2017年开始，水凝胶疲劳测试主要基于这类方法，对所测试的各类水凝胶的疲劳门槛值进行实验测试和理论分析。另一种疲劳测试方法是对不带裂纹试样进行循环加载拉伸至给定的拉伸比幅值λ或应力幅值，记录其断裂的循环数N（图1b）。当施加的拉伸比低于疲劳极限拉伸比λ_e时，试样被认为能够承受无数次循环拉伸而不发生断裂。本文采用第二类测试方法，以经典的双网络韧性水凝胶为对象，实验测量并分析材料的λ-N曲线特征，重点关注不含裂纹的试样的λ-N曲线和含不同裂纹尺寸的试样的λ-N曲线的不同，如图2所示。为了获得断裂循环次数的统计结果，采用六个相同的试样（不含裂纹或含相同尺寸的裂纹）同时拉伸的测试方法。

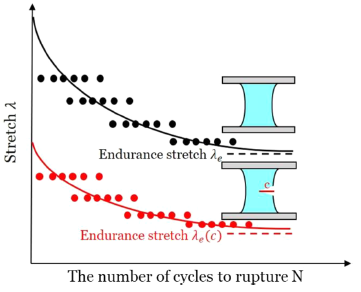
图2 疲劳测试的λ-N曲线。每次疲劳实验中，六个相同的试样（不含裂纹或含相同尺寸的裂纹）在给定的拉伸幅值下循环受载，每个试样的拉伸幅值和断裂循环次数对应图中的一个点。材料的疲劳极限拉伸比是试样中的初始裂纹尺寸的函数。

  研究发现，当初始裂纹较长时，韧性水凝胶的疲劳极限随着裂纹长度的增加而降低；当初始裂纹较短时，韧性水凝胶的疲劳极限对初始裂纹尺寸不敏感。测试结果表明该水凝胶在循环载荷下的裂纹敏感尺寸约为0.1mm。他们将这一敏感尺寸解释为材料的固有属性常数，称作endurance fractocohesive length，其大小由另外两个材料的固体常数决定，材料的疲劳门槛值G_th和材料在达到循环疲劳极限条件下的断裂功W_e(o)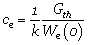，其中系数k由材料的本构关系和待测试样的几何特征决定。通过实验测量韧性水凝胶的疲劳门槛值和循环疲劳极限条件下的断裂功，代入如上公式估算得到的该材料的裂纹敏感尺寸为0.1mm量级，与实验相符。他们还讨论了各类工程材料在循环载荷下的这两个材料常数的取值范围以及所对应的裂纹敏感尺寸。

实验结果

1 单轴拉伸下的断裂

  他们采用聚丙烯酰胺(PAAm)-聚-2丙烯酰胺-2甲基丙磺酸(PAMPS)双网络韧性水凝胶进行裂纹敏感性测试。他们先单调拉伸不带裂纹以及带裂纹的水凝胶试样，获得不同裂纹长度对应的应力-拉伸比曲线，断裂拉伸比λ_c，断裂应力S_c以及断裂功W_c（由积分应力-拉伸比曲线得到），这些断裂属性都是裂纹长度c的函数。当初始裂纹较小时（65μm），测量的断裂属性与无预置裂纹的试样相近，而当初始裂纹较大时，断裂属性随裂纹长度增加而明显降低。

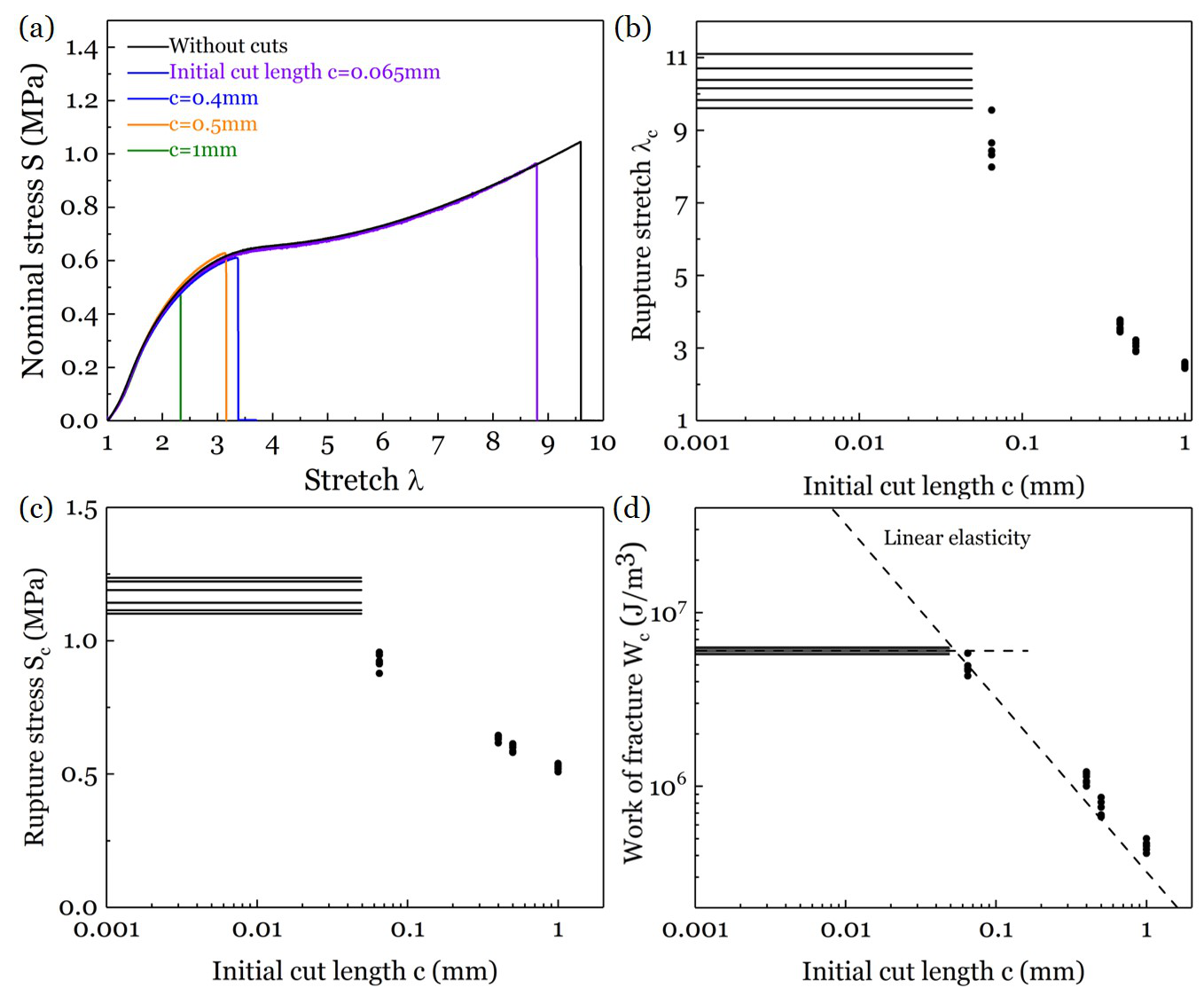
图3 承受单调拉伸的不带裂纹的试样以及带不同长度裂纹的试样的断裂。(a)应力-拉伸比曲线。(b)断裂拉伸比-裂纹长度平面。(c)断裂应力-裂纹长度平面。(d)断裂功-裂纹长度平面。

  他们通过变异系数CV（标准差除以平均值）来衡量测量数据的分散性。无论是带裂纹试样还是不带裂纹试样，断裂拉伸比λ_c，断裂应力S_c，断裂功W_c以及刚度M的变异系数都很小(小于0.1)。尤其是，断裂属性的分散性程度与材料的刚度分散性相当，因此可以认为所测量的材料属性为材料常数。由此得到，不带裂纹试样的断裂功这一材料常数W_C(o)为5.87×10⁶J/m³。该韧性水凝胶的另一材料常数断裂能在此前的工作中测量G_C=2550J/m²。

图4 单调载荷下带裂纹与不带裂纹试样的断裂拉伸比，断裂应力，断裂功以及刚度的变异系数。

  对于带裂纹试样且裂纹长度远小于试样尺寸，能量释放率G有G=κWc，其中c为裂纹长度，W为远离裂尖的弹性能密度，κ为一个无量纲数。当试样断裂时，断裂能G_c有G_c=κW_cc。材料裂纹敏感尺寸可由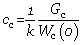得到。当材料为线弹性且试样为边缘裂纹时，κ的值为2π(1.122)²，由此得到该材料在单调载荷下的裂纹敏感尺寸为0.05mm，与实验观测到的裂纹尺寸敏感性基本相符。

2 循环拉伸下的断裂

  他们循环拉伸不带裂纹以及带裂纹的水凝胶试样，获得不同裂纹长度对应的疲劳极限下的应力-拉伸比曲线，疲劳极限拉伸比λ_e，疲劳极限应力S_e以及疲劳极限条件下的断裂功W_e，这些疲劳极限属性都是裂纹长度c的函数。当初始裂纹较小时（65μm），测量的疲劳极限属性与无预置裂纹的试样相近，而当初始裂纹较大时，疲劳极限属性随裂纹长度增加而明显降低。不带裂纹试样在疲劳极限条件下的断裂功W_e(o)这一材料常数为1.02×10⁵J/m³。该韧性水凝胶的另一材料常数疲劳门槛值在此前的工作中测量为G_th=114.2J/m²。

  对于带裂纹试样且裂纹长度远小于试样尺寸，能量释放率G有G=κWc，当试样达到疲劳极限时，疲劳门槛值G_th有G_c=κW_ec。循环载荷下材料裂纹敏感尺寸可由得到。当材料为线弹性且试样为边缘裂纹时，κ的值为2π(1.122)²，由此估算得到该材料在循环载荷下的裂纹敏感尺寸为，与实验观测到的裂纹尺寸敏感性基本相符。

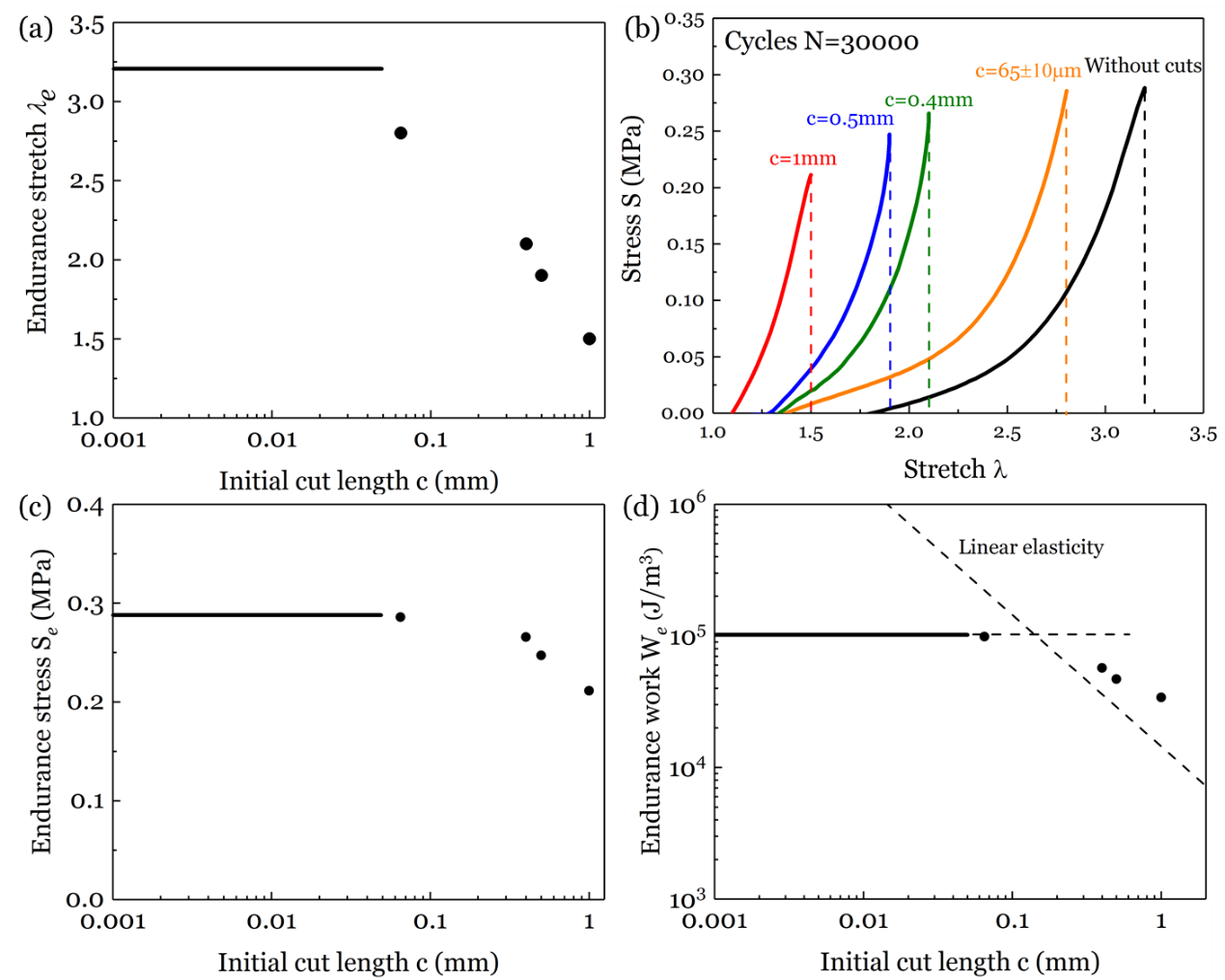
图5 承受循环拉伸的不带裂纹的试样和带不同长度裂纹的试样的疲劳极限。(a)疲劳极限拉伸比-裂纹长度平面。(b) 达到疲劳极限时的应力-拉伸比曲线。(c)疲劳极限应力-裂纹长度平面。(d)疲劳极限条件下的断裂功-裂纹长度平面。

3 材料属性空间

  承受循环载荷时，当初始裂纹长度大时，试样抵抗裂纹扩展的能力用疲劳门槛值G_th描述。当初始裂纹长度小，对裂纹不敏感时，抵抗疲劳断裂用不带裂纹试样在疲劳极限条件下的断裂功描述W_e(o)。研究人员从文献中收集得到弹性体，塑料，陶瓷，金属的G_th和W_e(o)数据。这两个材料常数的比值定义了endurance fractocohesive length，用斜虚线表示。陶瓷的endurance fractocohesive length在10^-4m这个量级。金属和文中的韧性水凝胶的endurance fractocohesive length在10^-3m这个量级。

图6 用不带裂纹试样测得的疲劳极限条件下的断裂功W_e(o)与用带裂纹试样测得的疲劳门槛值G_th构成的材料属性平面。斜虚线为endurance fractocohesive length,G_th/W_e(o)。

4 结论

  他们研究了双网络韧性水凝胶带裂纹与不带裂纹、在单调载荷和循环载荷下的断裂行为。单调载荷下，测试了不同裂纹长度c对应的断裂拉伸比λ_c，断裂应力S_c以及断裂功W_c。当初始裂纹较短时，断裂功是材料常数，W_c(o)，对初始裂纹不敏感。当初始裂纹较长，断裂能是材料常数G_c。两个材料常数的比值定义了另一材料常数fractocohesive length，G_c/W_c(o)，单调载荷下裂纹敏感尺寸为。循环载荷下，他们测试了不同裂纹长度c对应的疲劳极限拉伸比λ_e，疲劳极限应力S_e以及疲劳极限条件下的断裂功W_e。当初始裂纹较短时，疲劳极限条件下的断裂功是材料常数，W_e(o)，对初始裂纹不敏感。当初始裂纹较长，疲劳门槛值是材料常数G_th。两个材料常数的比值定义了另一材料常数endurance fractocohesive length，G_th/W_e(o)，循环载荷下裂纹敏感尺寸为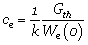。循环载荷下软材料的裂纹敏感尺寸这一重要的材料参数对指导抗疲劳软结构的设计具有重要意义。

这一研究工作最近发表在Journal of the Mechanics and Physics of Solids。论文的第一作者为西安交通大学航天航空学院博士研究生周一帆，西安交通大学卢同庆教授和美国科学院院士、美国工程院院士、哈佛大学锁志刚教授为共同通讯作者。

  原文链接：

  Zhou et al. Flaw-sensitivity of a tough hydrogel under monotonic and cyclic loads. Journal of the Mechanics and Physics of Solids. 2021.

  https://doi.org/10.1016/j.jmps.2021.104483

1.Zhang WL, et al. (2018) Fatigue of double-network hydrogels. Engineering Fracture Mechanics 187:74-93.

2.Zhang W, et al. (2019) Fracture Toughness and Fatigue Threshold of Tough Hydrogels. ACS Macro Letters 8(1):17-23.

3.Zhou Y, et al. (2020) The Stiffness-Threshold Conflict in Polymer Networks and a Resolution. J Appl Mech-T Asme 87(3):031002.

4.Zhang W, Gao Y, Yang H, Suo Z, & Lu T (2020) Fatigue-resistant adhesion I. Long-chain polymers as elastic dissipaters. Extreme Mechanics Letters 39.

5.Zhang W, Hu J, Yang H, Suo Z, & Lu T (2021) Fatigue-resistant adhesion II: Swell tolerance. Extreme Mechanics Letters 43:101182.