预测材料的断裂对工程应用十分重要。对于给定的材料，断裂的条件例如断裂应力、断裂应变，通常在不同试样间分布很广，其中小概率断裂的条件与断裂的平均值往往偏离很大。然而小概率断裂的条件对工程师进行结构设计意义重大。为了观测小概率断裂，工程师必须在相同条件下测试大量的试样，非常耗时。一个可能的解决方案是进行高通量实验。高通量实验已较为广泛的应用于化学、热、电和生物性能的测量，但目前很少用于材料力学性能的测量。因此，西安交通大学卢同庆教授与哈佛大学锁志刚教授、斯坦福大学Jose Blanchet教授合作，共同开发了一种用于预测材料小概率断裂的高通量实验。在设计的高通量实验中，研究者在相同环境下打印制备了1000个试样，将他们拉伸到相同的拉伸比，通过处理实验录像自动识别每个试样的断裂。高通量实验产生的大量断裂数据使得运用数学中的极值概率理论分析成为可能。

1. 高通量实验设计及图像处理识别断裂

  他们开发了一个高通量实验来研究小概率材料断裂与疲劳(图1)。他们在相同的条件下打印了1000个哑铃型试样。设计了一种单自由度的运动机构，使所有的试样在同一时间发生相同的变形。对于数量如此之多的试样，用人眼来识别单个试样的断裂是不现实的。他们记录了每次实验的视频，并编写了处理视频的软件，以识别每个试样的断裂。

  实验装置包括一个运动机构、一个带控制盒的电动位移台、一个摄像机和一台计算机(图1b)。运动机构由连接六块铝板的菱形支架组成。通过氰基丙烯酸酯胶水，每块铝板与一个打印的矩形连接部分粘接。运动机构的两端固定在电动位移台的两个刚性夹具上，由控制箱提供动力并进行控制。连杆与铝板通过螺钉、螺母、轴承连接。拉伸时，试样沿拉伸方向伸长，铝板沿拉伸方向进行刚体平移，连杆绕铰链转动。该运动机构与两个单自由度的夹具一起运动，同时将所有1000个试样拉伸至同一拉伸比。在实验中，他们通过摄像机记录所有1000根试样的拉伸过程，然后将每幅图像处理成一个灰度矩阵来进行试样断裂的图形后处理。

图1 实验方法。(a)示意图。单自由度运动机构同时将大量试样拉向同一拉伸比，摄像机记录实验过程。(b)实验装置的照片。

2. 单调拉伸下的断裂及极值理论分析

  他们首先对1000个试样进行了单调拉伸测试。用三个照片展示1000个试样在单轴拉伸下的断裂。在未拉伸的状态下，这1000个试样没有断裂(图2a)。在拉伸比为1.8时，34个试样破裂(图2b)。在拉伸比为2.2时，947个试样破裂(图2c)。

图2 1000个试样在单轴拉伸下的断裂。

  这个实验重复了四次。他们将四次实验的数据进行汇总。对于给定拉伸比λ, 设 F 为断裂试样数量除以试样总数（4000）。 他们绘制累积分布函数F（λ），每个断裂的试样对应F - λ平面内一个数据点(图3a)。根据断裂统计的经验，他们用三参数Weibull分布来拟合: 

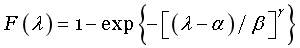
  其中 α，β与γ为分布，尺度与形状参数。通过最大似然估计法拟合三个参数，并对于任一给定的累计概率函数计算95%置信区间。高度可信的拟合结果要求大多数数据落在95%置信区间内，准确的拟合结果要求95%置信区间很窄。实验测得的累积分布函数在全数据范围内近似服从Weibull分布(图3a)。计算得到的95%置信区间虽然窄，但是许多数据点落在置信区间外，Weibull分布不能很好地拟合全体实验数据。

  为了研究小概率断裂，他们将图14a中的区域放大(图3b)。与全局拟合类似，大量数据落在95%置信区间外。也就是说，使用所有4000个测试试样数据的Weibull分布拟合无法在具有较高置信度的前提下预测包括小概率事件在内的实验数据。

  他们采用Peak-over-threshold方法来获得准确可靠的小概率断裂预测。采用Peak-over-threshold方法后，4000个试样中只有率先断裂的255个试样用于Weibull分布拟合。使用这个方法后，所有数据点均落在95%置信区间里(图3c)。例如，他们定义一个小概率事件 F（λ）= 0.1%, 对应于4000个试样中先断裂的4个试样。对于“0.1%断裂”的小概率事件，测得的断裂拉伸比为 λ= 1.7111，Weibull拟合结果为  λ= 1.7166，95%置信区间为1.7056 < λ < 1.7288。在95 %的高置信度下，拉伸比拟合区间很窄，该预测精度能够满足大多数应用。通过Peak-over-threshold 方法，Weibull分布能够预测小概率断裂。

  通常来说，获得4000个断裂试样的断裂数据是不可能的，工程师只能使用少量的测试试样来预测小概率断裂。他们通过随机选取试样来模拟少量试样的情况。从4000个数据中随机选取的200，500,1000个试样，采用同样的Peak-over-threshold方法，所有小概率断裂试样均落在95%置信区间内，随着试样数量的增加，95%置信区间越来越窄。（图3d, 3e, 3f）。大的数据集使得小概率事件的预测同时高度可信和准确。

图3 单轴拉伸下的断裂概率。

3. 循环拉伸下的断裂及极值理论分析

  他们对1000个试样进行了循环拉伸。进行四次实验，拉伸幅值λ分别为1.6，1.7，1.8，1.9。每次1000个试样的循环拉伸下的断裂都以四张照片进行展示 (图4)。例如，在规定拉伸幅值λ为1.6的试验中，第一次循环没有试样断裂，500次循环后7个试样破裂，1000次循环后49个试样断裂，3万次循环后只有4个试样没有断裂。通过对所记录的视频图像进行处理，可以得到单个试样的断裂循环次数N。

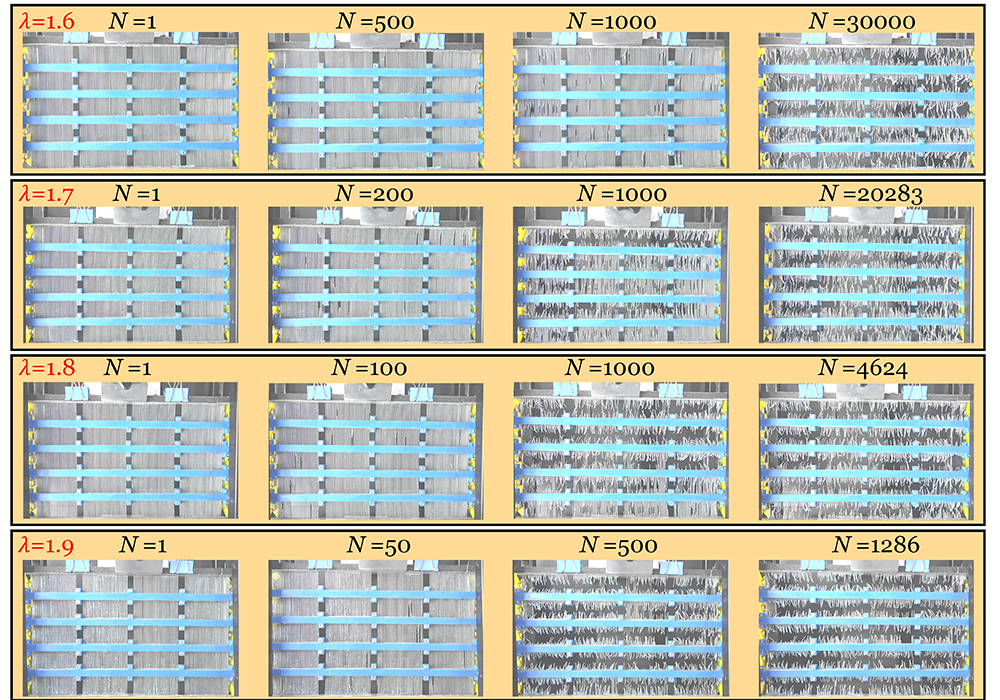
图4 试样在循环拉伸下的断裂。

  他们用累积分布函数F_λ（N）来表征疲劳断裂的概率，定义为在给定的拉伸幅值λ下，断裂试样的数量除以总试样数量(图5a)。对于每个拉伸幅值λ，使用三参数Weibull分布拟合累积分布函数F_λ（N）:

  他们同样通过最大似然估计法拟合三个参数，并计算95%置信区间。实验数据与Weibull分布结果大致吻合，但许多数据点落在95%置信区间外（图5a），Weibull分布不能很好地拟合全体数据。为了研究小概率疲劳断裂，他们将图5a中的区域放大，并只保留拉伸幅值λ为1.6的数据(图5b)。与单调加载一样，同样大量数据落在95%置信区间外，Weibull拟合不能很好地小概率预测疲劳断裂。他们接着只把率先断裂的200个试样用于拟合，所有数据点均落在95%置信区间里（图5c）。例如对于一个“1%疲劳断裂”的小概率事件，也就是1000个测试试样中前10个断裂的试样，测得的疲劳寿命是 N= 517，Weibull拟合结果为 N= 566，95%置信区间为480 < N < 701。在95 %的高置信度下，循环次数拟合区间很窄，该预测精度能够满足大多数应用。大的数据集使得小概率事件的预测同时高度可信和准确（图5c）。

  对于疲劳断裂来说获得大量数据是更困难的。文献中通常只有几十个试样的数据。为了模仿常见做法，他们从1000个数据中随机选取50个试样，只用前10个断裂的试样进行拟合。为了检验对小概率事件的预测，他们在该范围内绘制了所有1000个测试试样中的断裂的试样。取50个试样比较随机，重复进行三次（图5d，5e，5f）。三种拟合结果显示出明显的不一致性:有时实验数据在95%置信区间外(图5e)，有时95%置信区间很宽(图5f)。就Weibull统计而言，小数据集无法使小概率事件的预测同时高度可信和准确。

图5 循环拉伸下的断裂概率。

4. 小结

  他们发展了一种能够同时对大量试样进行断裂/疲劳测试的高通量实验装置来研究小概率断裂。每一次实验，他们在相同的条件下打印1000个试样，拉伸到相同的拉伸比，通过图像处理实验视频，自动识别单个试样的断裂。在单调荷载下，记录每个试样的断裂拉伸比；在循环荷载下，记录每个试样断裂循环次数。利用Weibull分布和Peak-over-threshold方法研究了小概率断裂。研究表明，预测小概率事件需要大量的数据，而高通量实验使得对小概率事件的预测具有较高的准确性和可信度。

  这一研究工作最近发表在Matter。论文的第一作者为西安交通大学博士研究生周一帆和斯坦福大学博士研究生张旭辉，西安交通大学卢同庆教授，美国两院院士、哈佛大学锁志刚教授和斯坦福大学Jose Blanchet教授为共同通讯作者。论文第一单位为西安交通大学机械结构强度与振动国家实验室软机器实验室。

  原文链接：

  Zhou et al. High-throughput experiments for rare-event rupture of materials. Matter. 2022. 

  https://www.sciencedirect.com/science/article/abs/pii/S2590238521006755?dgcid=author