褶皱在软材料表面十分寻常，譬如皮肤上的皱纹，包子上的褶痕，和挤橡皮时的细纹（图1a-c）。褶皱亦有重要的应用前景，譬如生物分子的动态呈现[1]（图1d），以及神经突的诱导生长[2]（图1e）。

图1. 褶皱在软材料表面十分寻常亦有重要的应用前景。a. 皮肤上的皱纹（图为罗中立油画《父亲》）。b. 包子上的褶痕。c. 挤橡皮时的细纹。d. 利用褶皱动态呈现生物分子[1]。e. 利用褶皱诱导神经突的生长[2]。

  褶皱虽寻常却并不平凡。相应的力学研究虽历时五十余载，仍不能与实验完全吻合。早在1963年， Biot曾做过橡胶受压失稳的线性分析并推导出临界应变为0.46（平面应变条件，下同）[3]。及至1999年，Gent的实验却发现褶皱总在应变0.35时发生，远低于Biot的预测[4]。直到2008年，Mahadevan和他的博士生Hohlfeld才解决这一分歧[5]。他们指出软材料中的褶状皱（crease）和Biot所研究的波状皱（wrinkle）是两种不同的失稳模态（图2）。波状皱是弥漫整个表面的光滑起伏。波的幅度可以无限减小而趋近平表面，随之整个材料中的应变也一致趋于零，故波状皱的失稳可以通过对平表面进行线性摄动来分析。褶状皱是局限一处的陡峭折叠，其底端是一道尖锐的折痕。褶的深度可以无限减小而趋近平表面，但是应变在尖锐的褶底总是发散的，故褶状皱的失稳需要非线性模拟来分析。Hohlfeld和Mahadevan的理论成功预测了橡胶上褶皱的临界应变。然而橡胶在软材料中偏硬（剪切模量~1MPa）。更软的材料中，譬如水凝胶和生物组织（剪切模量~1kPa或更低），褶皱现象仍扑朔迷离。在这些更软的材料中，表面张力不容忽视地影响着表面形貌，亦即所谓的毛细弹性现象（Elastocapillarity）[6]。2011-2012年间Mora等人[7]和陈大勇等人[8]分别研究了毛细弹性褶皱。然而两个组得出的结论却大相径庭：Mora等人的观测非常接近经过毛细弹性修正后的波状皱模型。而陈大勇等人的观测却要用毛细弹性修正后的褶状皱模型来拟合，其临界应变远低于相应的波状皱模型。

图2. 波状皱和褶状皱的差别。波状皱是弥漫整个表面的光滑起伏。褶状皱是局限一处的陡峭折叠。

  近日，哈佛大学锁志刚教授组和麻省大学Hayward教授组合作用全新的毛细弹性褶皱模型（Elastocapillary Crease）解决了上述冲突。该模型可以用图3所示的后屈曲路径来表示。因为表面张力总倾向使表面光滑，前述有尖锐底部的褶状皱将被抑制。有表面张力时，Hohlfeld和Mahadevan所预测的褶状皱分岔点不复存在。弹性体最终在波状皱分岔点失稳（图3蓝绿路径交点，临界应变ε_w ）。分岔之后的波状皱并不稳定，会发生折叠（图3橙色路径 ）并形成褶状皱（图3红色路径）。具体折叠路径与表面发生接触之后表面张力的变化有关，图3是假设表面接触后无张力的特例。褶状皱临界应变（ε_c ）被定义为褶状皱存在的最低应变，亦即褶状皱由不稳定变为稳定的拐点（图3红色路径的拐点，实线和虚线的转换点）。该拐点所对应的褶皱深度由模型中唯一的特征尺度——毛细弹性尺度——决定。毛细弹性尺度的定义为表面张力γ和剪切模量μ之比γ/μ。

图3. 毛细弹性褶皱的后屈曲路径图。图中实线为稳定路径，虚线为不稳定路径。蓝色路径对应平表面。绿色路径对应波状皱。橙色路径对应波状皱到褶状皱的折叠过程。红色路径对应褶状皱。

  上述后屈曲路径意味着褶皱形成的应变对缺陷敏感（图4）。毛细弹性模型中，只有γ/μ一个特征尺度。若缺陷尺寸d<<γ/μ，表面张力可以抹平缺陷。系统会在接近波状皱分岔点（ε_w ）的应变失稳，并突跳到相同应变的稳定路径上。若缺陷尺度d>>γ/μ，应力集中可使缺陷处形成浅小的褶状皱，即便整体应变很低。当应变接近褶状皱临界应变（ε_c ）时，缺陷处浅小的褶状皱可以加深增长，发展成实验上可观测的失稳。对于任意尺度的缺陷，失稳点都会在这两个极限之间。也就是说，褶皱的失稳永远发生在一个确定的应变区间，其上下界分别为ε_w和ε_c。

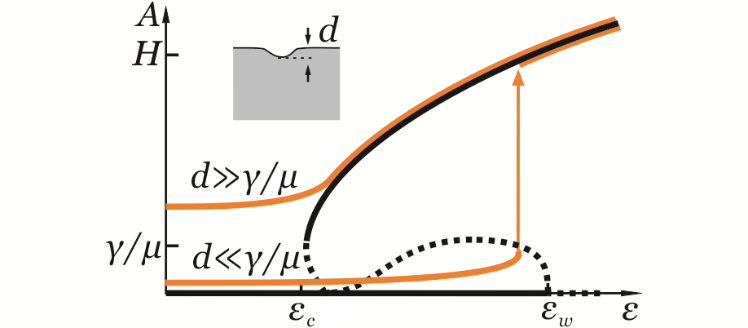
图4. 毛细弹性褶皱的缺陷敏感性。大缺陷导致接近褶状皱临界应变（ε_c ）时的失稳。小缺陷导致接近波状皱分岔点（ε_w ）时的失稳。

  褶皱失稳的应变区间可以被实验测量。图5中汇总了文中新采集的数据与之前文献中报道的数据。正如理论所预测，软材料褶皱的失稳是对缺陷敏感的，并且总发生在理论预测的应变范围内。

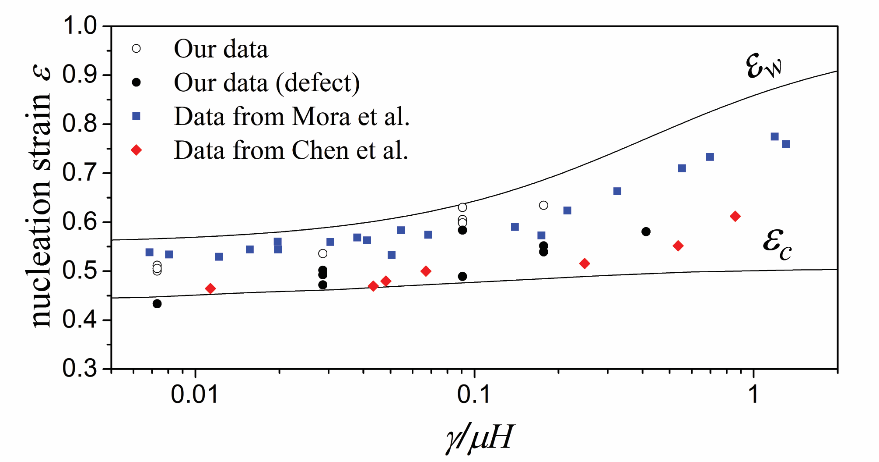
图5. 实验验证预测的失稳区间。H是样品的初始厚度。

  该研究工作发表在Physical Review Letters上，并获编辑推荐（Editors’ Suggestion）。刘綦涵博士与Tetsu Ouchi博士为共同第一作者。哈佛大学锁志刚教授与麻省大学Ryan Hayward教授为共同通讯作者。

参考文献

1. Kim, J., J. Yoon, and R.C. Hayward, Dynamic display of biomolecular patterns through an elastic creasing instability of stimuli-responsive hydrogels. Nature materials, 2010. 9(2): p. 159.

2. Saha, K., et al., Surface creasing instability of soft polyacrylamide cell culture substrates. Biophysical journal, 2010. 99(12): p. L94-L96.

3. Biot, M.A., Surface instability of rubber in compression. Applied Scientific Research, Section A, 1963. 12(2): p. 168-182.

4. Gent, A. and I. Cho, Surface instabilities in compressed or bent rubber blocks. Rubber Chemistry and Technology, 1999. 72(2): p. 253-262.

5. Hohlfeld, E.B., Creasing, point-bifurcations, and the spontaneous breakdown of scale-invariance. 2008: Dissertation.

6. Style, R.W., et al., Elastocapillarity: Surface tension and the mechanics of soft solids. Annual Review of Condensed Matter Physics, 2017. 8: p. 99-118.

7. Mora, S., et al., Surface instability of soft solids under strain. Soft Matter, 2011. 7(22): p. 10612-10619.

8. Chen, D., et al., Surface energy as a barrier to creasing of elastomer films: An elastic analogy to classical nucleation. Physical review letters, 2012. 109(3): p. 038001.

论文信息与链接：

Qihan Liu, Tetsu Ouchi, Lihua Jin, Ryan Hayward, and Zhigang Suo, Elastocapillary Crease. Physical Review Letters, 2019. 122(9): p. 098003.

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.122.098003