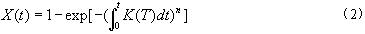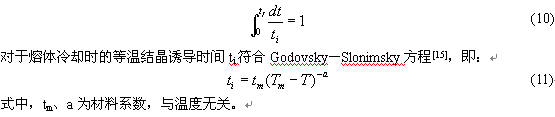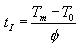陶四平，于润泽，周明，冯建民，杨鸣波*
（四川大学高分子科学与工程学院，高分子材料工程国家重点实验室，四川 成都 610065）
收稿日期：基金项目：国家自然科学基金重点项目资助(29934070)
作者简介：杨鸣波 (1957-), 教授, 博导. 研究方向: 高分子材料加工工程 * 通讯联系人

摘 要：通过差示扫描量热法对高密度聚乙烯的非等温结晶动力学进行了探讨，引入非等温结晶诱导时间后，比较了两种能描述聚合物在变温热历史下的结晶动力学，结果表明Nakamura法描述HDPE的结晶动力学与实验一致性比Dutta法好。在Nakamura模型中，结合线性回归分析和试差法，找到了能直接从非等温结晶实验中获取HDPE的结晶动力学参数的方法。
关键词：高密度聚乙烯；结晶动力学；诱导时间

    高密度聚乙烯（HDPE）作为一种半结晶型聚合物，由于物化性能优异、成型加工简易、价格相对便宜等优点，已广泛用于国民生产的各个领域，成为产量和需求量最大的一类合成树脂之一。
    通常，半结晶型聚合物在成型加工过程中由熔体等温或非等温冷却至特定形状的制品时都会产生晶体结构，这一微观结构往往又是控制制品性能好坏的重要因素，如刚度、韧性、透明度等。因此，为了寻求最佳的成型加工条件并获得最优性能的制品，定量探讨它们在成型加工过程中的结晶行为或结晶度的增长规律，已越来越受学者们关注[1-3]。为实现HDPE注射成型过程结晶行为的计算机模拟，本文意在获得HDPE的结晶动力学参数，同时通过其在不同冷却速度下结晶度变化的差示扫描量热法（DSC）实验值与理论值的比较，寻求能描述HDPE在快速冷却热历史下的结晶动力学的最佳形式。
1 理论基础
1.1 结晶动力学部分
Avrami[4]从金属结晶推出的等温结晶动力学，用在聚合物方面颇有成效，现已得到广泛应用。方程具体形式如下：

式中X(t)为t时刻的相对结晶度；n为Avrami指数，与成核及生长方式有关；T为等温结晶时的温度；k为等温结晶动力学速率常数，包括成核速率与晶体生长速率。
    但是，由于在实验中要实现等温结晶，需选取合适的结晶温度区间，这一温度区间往往比聚合物在实际加工过程中出现结晶的温度高，而不能准确反映出聚合物在加工过程中的结晶型为。因此有必要研究它们在变温情况下的非等温结晶动力学。目前，很多学者都是基于Avrami方程等温结晶出发，同时考虑非等温结晶的特点而修正得到的非等温动力学方程。
    Nakamura等[5,6]基于晶体生长速率与成核数率的比值与温度无关的假设，即等动力学条件下，将Avrami方程成功推广到变温情况下的相变过程，具体形式为：

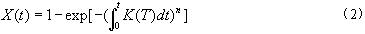
式中积分下限表示结晶起始时刻，计为0时刻；K(T)为温度T(t)下的非等温结晶动力学速率常数，K(T)=k(T)1/n。
    Isayev等[7]在分析聚对苯二甲酸乙二醇酯（PET）的非等温结晶时，引入Hoffman-Lauritzen形式[8]的速率常数，将Nakamura方程成功推广到降温速度为2到40℃·min-1下的结晶过程。


1.2 结晶诱导时间
    结晶诱导时间是指材料产生结晶行为、出现放热峰时的起始时间，对于聚合物而言，结晶放热峰可出现在熔体冷却时低于平衡熔点的某一温度，或在淬冷样品加热时高于玻璃化转变温度的某一温度。结晶诱导时间的引入对于成型加工过程中聚合物结晶行为的模拟非常重要[10,13]，因此已越来越受众多学者重视。
    一般认为，非等温结晶诱导时间tI与等温结晶诱导时间ti满足[14]：


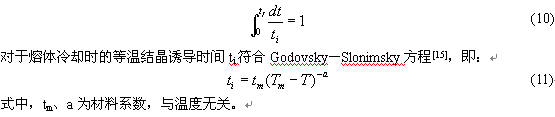
2 实验部分
    实验采用中国石油大庆石化公司生长的高密度聚乙烯，PE-LA-50D012(5000S)。实验时称取约10mg样品，在NETZSCH DSC204差示扫描量热计上以10℃·min-1速度升温到200℃，使样品熔融，保持4min以消除样品的热历史，分别在氮气保护下用不同冷却速度Φ＝5、10、11、14、15、20、40℃·min-1冷却至室温20℃，得到七种不同降温速率的DSC图谱。
    通过对DSC曲线上部分峰积分的方法可获得降温过程中不同时刻的结晶度：

算，对应变化可按下式进行：其中，ρa为完全无定型HDPE的密度，取0.857g·cm^-3；ρc为完全结晶HDPE的密度，取1.002g·cm^-3 [16]。

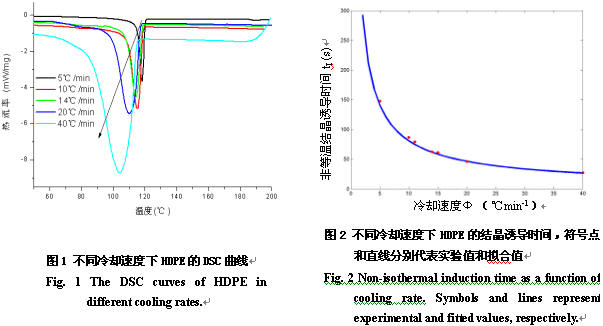
3 结果与讨论
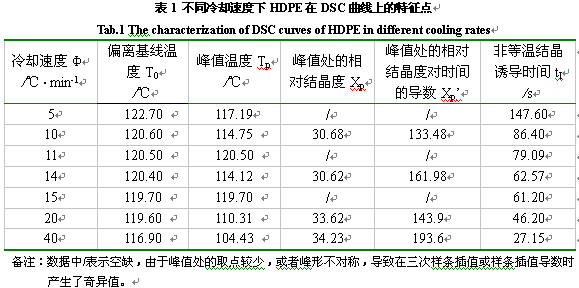
    图l为不同降温速率下HDPE的DSC曲线。随着降温速率的增大，结晶峰变宽，结晶起始温度T₀和结晶峰温度T_p都向低温方向变化。对DSC曲线峰部分，可通过三次样条插值获得峰值处相对结晶度Xp及相对结晶度对时间的导数X_p’.从图1中获得的特征点列于表1，可按前述理论部分进行HDPE的结晶动力学计算。 
    DSC曲线上降温过程中偏离基线的温度一般被认为是该冷却速度下的结晶起始温度，于是相对于材料的平衡熔点T_m，我们可得出该冷却速度下的表现结晶诱导时间t_I：

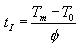
    将所得不同冷却速度下的表现结晶诱导时间代入式（10），并结合式（11）进行非线性回归，可得出HDPE的材料系数tm=5.29×105s·Ka，a=4，进而可获得HDPE在不同热历史下的非等温结晶诱导时间，（见图2）。可以看出，随着冷却速率的增大，结晶诱导时间变短，当冷却速率小于15℃·min-1时，冷却速率对结晶诱导时间的影响很大，而当冷却速率超过15℃·min-1之后，诱导时间对冷却速率的依赖性不是很明显。

    对DSC曲线特征点按Dutta法处理，可得HDPE的结晶动力学参数，Avrami指数n=2.3，结晶活化能Ed/R=4003.6K。拟合结果见图3，可以看出有较好的线性关系。将n和Ed值代入式（9），并针对不同冷却速度下相对结晶度X(t)和时间t的关系，可获得Dutta法中的指前因子A的平均值为0.001，将上述结晶动力学参数代入式（9），得到HDPE在不同热历史下相对结晶度对时间的关系。在等速降温的情况下，并引入非等温结晶诱导时间后，HDPE相对结晶度的模拟值与DSC上实验值的比较见图4。可以看出，理论值与实验值具有较好的一致性，但随着结晶的进行，两者的偏差略有增大，而且理论上HDPE完成结晶过程的时间相对实验值早。


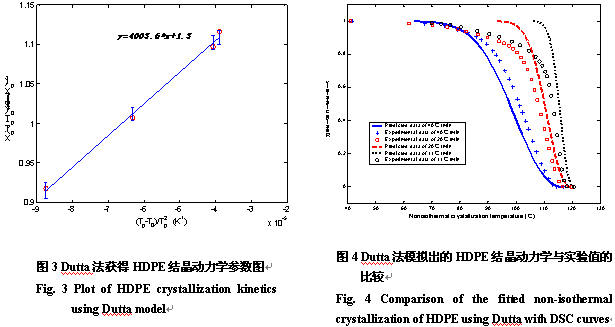
    将HDPE在不同冷却速度下的DSC数据，按式(5)处理，其中Kg分别取6×104、7×104、8×104、9×104K2，见图5中(a)、(b)、(c)、(d)，可以发现其中Kg取7×104K2时，不同冷却速度下log[-log(1-X(t))]对logf(t)作图具有一致的线性关系，因此本体系HDPE的Kg取7×104K2，将其代入式（5）中，并对冷却速度分别为20℃·min-1和40℃·min-1的DSC数据进行线性回归，可得C=400，n=1.3，回归系数R＝99％。其中Avrami指数n=1.3，我们认为是因为聚合物在结晶过程由于杂质、壁面等外界因素以及HDPE成核和生长形态的复杂性[17,18]所致。将上述结晶动力学系数代入式（2），可获得HDPE在不同热历史下相对结晶度对时间的关系。在等速降温热历史下，并引入非等温结晶诱导时间后，HDPE相对结晶度的模拟值与DSC上实验值的比较见图6。并比较图4后，可以看出用Nakamura法模拟HDPE的结晶动力学理论和实验值的一致性，比Dutta法好，因此Nakamura可较好地用于注射成型HDPE结晶行为的模拟，这为定量探讨结晶聚合物在成型加工过程中凝聚态结构变化奠定很好的基础。

4 结论
    1)针对DSC曲线的特点，引入非等温结晶诱导时间，获得了HDPE的材料系数，tm=5.29×105s·Ka，a=4。在此基础上得出了HDPE在不同热历史下的结晶诱导时间，这为确定HDPE在成型时的结晶起始时间提供了理论依据。
    2)通过对HDPE在不同冷却速度下结晶动力学的模拟值与DSC实验值的比较，得到了两种能描述聚合物在变温热历史下的结晶动力学形式，即Dutta法和Nakamura法，发现Nakamura法的模拟值与实验值具有更好的一致性。在Nakamura模型中，直接从HDPE的等速降温DSC实验上获得了材料的结晶动力学参数，根据log[-log(1-X(t))]对logf(t) 作图时与冷却速度的无关性，找出了H-L方程中Kg的最佳值，进而确定了其它的动力学参数。

参考文献:
[1]J-M Gonnet, J Guillet, J Sirakov, etc . “In-situ”Monitoring of the non-isothermal crystallization of polymers by dielectric spectroscopy[J]. Polymer Engineering and Science, 2002, 42(6): 1159 ~ 1170.
[2]C A Hieber . Modeling/Simulating the injection molding of isotactic polypropylene[J]. Polymer Engineering and Science, 2002, 42(7): 1387 ~1409.
[3]Dongman Choi, James L White . Comparison of structure development in injection molding of isotactic and syndiotactic polypropylenes[J]. Polymer Engineering and Science, 2002,42(8): 1642 ~ 1656.
[4]Avrami M J . Kinetics of phase change Ⅱ: transformation-time relations for random distribution of nuclei[J]. Journal of Chemical Physics, 1940, 8: 212 ~ 224. [5]K Nakamura, T Watanabe, K Katayama, etc . Some aspects of nonisothermal crystallization of polymers. Ⅰ. Relationship between crystallization temperature crystallinity, and cooling conditions[J]. Journal of Applied Polymer Science, 1972, 16: 1077 ~ 1091.
[6]K Nakamura, K Katayama, T Amano . Some aspects of nonisothermal crystallization of polymers. Ⅱ. Consideration of the isokinetic condition[J]. Journal of Applied Polymer Science, 1973, 17: 1031 ~ 1041.
[7]Chan T W, Isayev A I . Quiescent polymer crystallization: Modeling and measurements[J]. Polymer Engineering and Science, 1994, 34(6): 461 ~474.
[8]Rajen M Patel, Joseph E Spruiell . Crystallization kinetics during polymer processing-Analysis of available approaches for process modeling[J]. Polymer Engineering and Science, 1991, 31(10): 730 ~738.
[9]B A Wesson . Melt crystallization kinetics of syndiotactic polystryrene[J]. Polymer Engineering and Science, 1994, 34(14): 1157 ~1160.
[10]A J Isayev, J W Chan, K Shimoio, etc . Injection molding of semicrystalline polymers Ⅰ. Material Characterization[J]. Journal of Applied Polymer Science, 1995, 55: 807 ~819.
[11]A Dutta . Method to obtain Avrami parameters directly from non-isothermal crystallization data[J]. Polymer Communications, 1990, 31: 451 ~ 452.
[12]Haoyue Zhang Brian S Mitchell . A method for determining crystallization kinetic parameters from one nonisothermal calorimetric experiment[J]. Journal of Materials Research, 2000, 15(4): 1000 ~ 1007.
[13]X Guo, A I Isayev, L Guo . Crystallinity and microstructure in injection moldings of isotactic polypropylenes. Part 1: a new approach to modeling and model parameters[J]. Polymer engineering and science, 1999, 39(10): 2096 ~2114.
[14]W Sifleet, N Dinos, J R Collier . Unsteady-state heat transfer in a crystallizing polymer[J]. Polymer Engineering and Science, 1973, 13(1): 10 ~16.
[15]Godovsky Y K, Slonimsky G L . Kinetcs of polymer crystallization from the melt (calorimetric approach)[J]. Journal of Polymer Science. Polymer Physics Edition, 1974, 12(^), 1053 ~ 1080.
[16]桂祖桐, 谢建玲 . 聚乙烯树脂及其应用[M]. 北京: 化学工业出版社材料科学与工程中心, 2002 . 72 ~ 73.
[17]余坚, 何嘉松 . 聚合物熔体结晶的方式(Regime)理论[J]. 高分子通报, 2001, (1): 25 ~ 33.
[18]J D Hoffman, R L Miller . Kinetics of crystallization from the melt and chain folding in polyethylene fractions revisited: theory and experiment[J]. Polymer, 1997, 38(13): 3151 ~3212.


论文来源: 2005年塑料加工年会