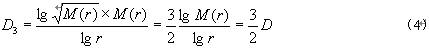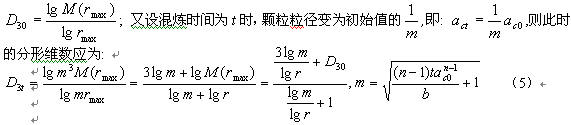PP/PS多相聚合物相形态演变及其机理研究
时间:2005-10-14
李云岩 盛京*
(天津大学材料科学与工程学院 天津 300072) *
shengxu@public.tpt.tj.cn
† National Nature Science Foundation of China(Grant No.50390094)
本文研究了聚丙烯/聚苯乙烯共混过程中相发展过程,讨论了分散相颗粒尺寸及其分布的变化规律,以分散相脆性破裂理论为基础,建立了分形维数的数学模型,通过比较该理论模型结果与试验结果,证明了共混中分散相破碎具有脆性破碎的特征。
若混炼过程中分散相破碎具有脆性破碎的特征, 则分散相颗粒尺寸变化满足[1]:
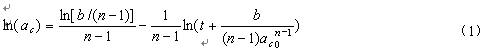
a
c0为初始时刻的颗粒尺寸,t为混炼时间。式(1)描述了分散相颗粒的粒径与时间的关系,暂称为”分散理论”,其中n和b成为分散系数。可建立分散相破碎的理想模型 (图1) 。
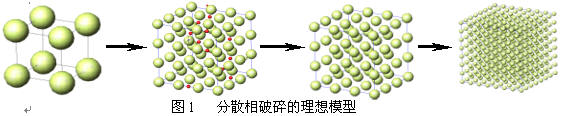
在二值化SEM图像上创建不同边长r的正方形,记录该正方形中所包含的分散相颗粒数M(r) ,根据分形理论可按式(2)求得分形维数[2]。

在研究自然界中实际分形的时候,首先必须判断所研究的对象是否确实分形,为此引入标度函数S(L)来研究对象的复杂程度。

若随着L的变化,S(L)为恒定值,则表示研究对象的复杂程度不随标尺的变化而变化,即它具有无标度性,或自相似性。通过此种方法求得的是SEM图像中分散相颗粒分布的分形维数,改值处于0~2范围内, 基于整个体系具有空间上的自相似性,可根据式(2)推导出分散相颗粒在三维空间分布的分形维数D3。
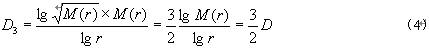
为研究高分子共混中分散相破碎机理, 建立了分散相破碎机理与分形行为关系。若分散相破碎属脆性破裂, 不妨建立分散相破碎的理想模型,如图1. 假设分散相颗粒的初始尺寸为ac0,所创建的正方体的最大边长为rmax, 该正方体包含的颗粒数为M(rmax),则此时的分形维数为:
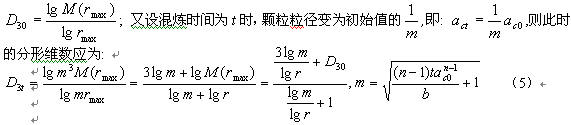
由于n, b值与加工条件及材料性质有关,这样就建立了分形维数与加工条件等因素相关的数学模型, 可通过比较分形维数的实验值和计算值对该模型及断裂机理进行讨论。
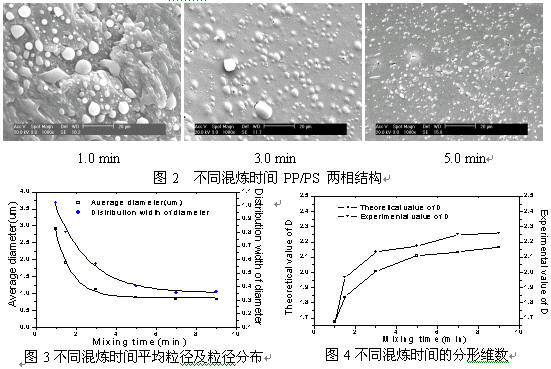
随着混炼时间的增加,分散相颗粒的粒径及其分布宽度逐渐减小,分散相的分布具有自相似性,分形维数逐渐增大并在混炼后期稳定下来,分形维数的实验值与理论值具有一致的变化规律,说明分散相的破裂确有脆性破裂的特征。
参考文献 [1] 周家敏.多组分多相聚合物共混过程在线分析.天津大学硕士论文,1996,115-116
[2] Takayasu H. Fractals in the physical sciences; Manchester university Press: Manchester and New York, 1990, 11-17
论文来源:2004年全国高分子材料科学与工程研讨会论文集